
The image fidelity achievable from a machine vision camera is only as good as the optics you use! Many of the machine vision cameras used today utilize very small pixels, down to 1.25um. The crispness of the images are a result of the resolution of your machine vision lens, so matching the right lens to the camera sensor is extremely important. We classify the lens resolution in terms of line pairs per millimeter (lp/mm). So, what lenses can help resolve these small pixels?
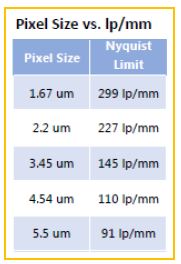
First, the relationship of pixel pitch can be put in terms of lp/mm as seen in the chart to the right. Machine vision lens manufacturers today typically provide the resolving power on their data sheets to help in the lens selection and ensure your matching the lens to the image sensor. If not matched properly, image contrast will suffer.
For machine vision cameras with small pixels, the Moritex ML-M-UR “Ultra high” resolution lenses are an excellent choice with the capability of resolving pixel pitches down to 2.2um with good contrast.
Click HERE for specifications on the Moritex ML-M-UR series and request a quote
The comparison images below show the Moritex ML-M-UR series compared to a conventional lens with less resolution. As you can see in the cutout of the corner, the contrast is much higher with lenses with high resolving power.

Lens resolution typically has fall off to the edges of a lens. To maintain high contrast, Moritex has optimized the ML-M-UR series to have good resolving power to the edges of the lens.
The charts below represent the contrast (MTF) corresponding to image height (x-axis ) showing the contrast from lens center to lens edge. The X-axis represents the center starting at zero millimeters and mapping MTF to the edge (furthest right point) The ML-M-UR shown in the left chart demonstrates very good performance across the lens. (A relatively flat line is good!) As a comparison to another lens (right chart), contrast is degraded across the lens from center to edge.
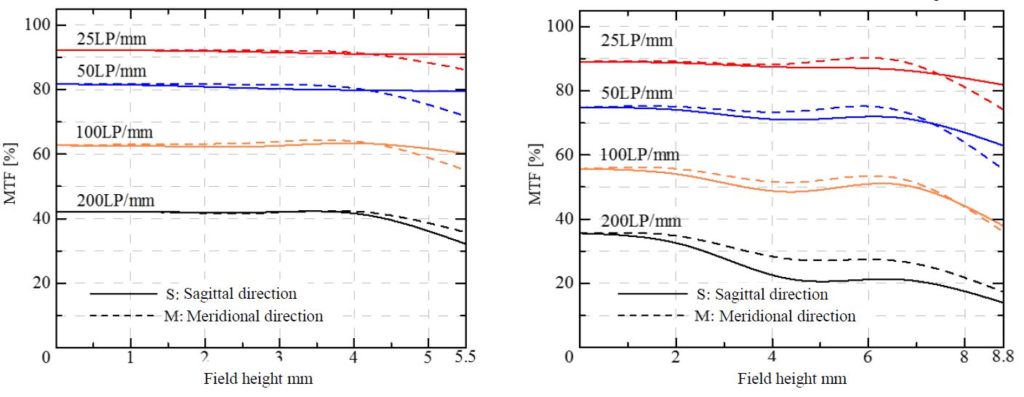
Aside from high resolution, The Moritex ML-M-UR series are a compact, 29mm diameter design and well suited for typical 29mm cube cameras. Additionally the lenses have an anti-vibration design with maximum acceleration to 10G’s.

discuss camera options.
1st Vision’s sales engineers have over 100 years of combined experience to assist in your camera selection. With a large portfolio of lenses, cables, NIC card and industrial computers, we can provide a full vision solution!
Ph: 978-474-0044 / info@1stvision.com / www.1stvision.com
Related Blog posts











 For this application, a liquid lens is used in conjunction with a telescentric lens taking images through different heights of the lens stack.
For this application, a liquid lens is used in conjunction with a telescentric lens taking images through different heights of the lens stack. 

